Ein 3-dimensionales Objekt muß im allgemeinen für Rendering und Raytracing im karthesischen Koordinatensystem beschrieben sein. Dazu müssen die in 3.1 expliziten Kugelfächenfunktionen, die in Polarkoordinaten gegeben, sind in karthesische umgerechnet werden.
4.2.1 ISO-Oberflächen, Rendering und Raytracing
IDL arbeitet mit dem Prinzip der ISO-Oberflächen. ISO-Oberflächen werden gebildet in dem Voxel mit der gleichen (vorgegebenen) Dichte miteinander verbunden werden. Die (ISO-) Oberfläche wird in IDL durch Polygone und Vertexe beschrieben.
Diese Listen entsprechen dem RAW-File-Format und können daher einfach als RAW-Files ausgeschrieben werden und in beliebige Raytracing-Programme übernommen werden.
Der Nachteil bei diesem Verfahren ist der extreme Rechenaufwand, da man im allgemeinen Dichtewerte für das gesamte Volumen, d.h. für jedes Voxel, berechnen muß. Bei ungefähr sphärischer Dichteverteilung kann man sich auf einen bestimmten Bereich beschränken, und einen Teil der Voxel mit einem beliebigen Dichte belegen, bei komplexeren Dichteverteilungen führt dies aber zu Verbindungsfehlern zwischen den Voxel.
Dieses Verfahren ist extrem rechenzeitaufwendig, da man zum Beispiel für einen Würfel mit einer Seitenlänge von 100 Einheiten 1 Million Berechnungen benötigt, für 220 Einheiten bereits 10 Millionen.
Genauso verhält sich die Rechenzeit für das Durchsuchen nach Voxel gleicher Dichte. Während sich die Rechenzeit mit der Auflösung hoch 3 erhöht, gewinnt man nur Qualität zum Quadrat.
4.2.2 Die Volumina für die ISO-Oberflächendarstellung:
Da die Körperdarstelung in IDL über VOXEL gleicher Dichte erfolgt, müssen die obigen Formeln für die Radien der verschiedenen Pulsationsmoden in karthesiche Koordinaten übertragen und eine Dichtefunktion für das Volumen definiert werden.
Die Definition der Dichtefunktion ist die Schlüsselüberlegung dieses Teils da mit dieser die Natur der Pulsation beschrieben wird. Der Dichtefunktion liegt die folgende Überlegung zu Grunde:
Den Punkten, die am mittleren Radius liegen können wir die Dichte zuteilen die der Entfernung zum Zentrum entsprechen. Punkten die über dem mittleren Radius liegen müssen wir Dichtewerte zuordnen, die kleiner sind als es ihrer Entfernung vom Zentrum und eben der gerade genannten entspricht. Und analog ordnen wir jenen die innerhalb des mittleren Radius liegen eine größere Dichte zu, als es ihrer Entfernung vom Zentrum entspricht.
Das bedeutet, daß sich die Dichte umgekehrt proportional zur Abweichung von der Kugelsymmetrie verhält.
Es genügt daher einem VOXEL V(x,y,z) genau jenen Dichtewert zu zuordnen, der seiner Entfernung im ungestörten Zustand entspricht:
wobei:
... der Kugelsymmetrie entspricht,
... der Oberfläche des Pulsierenden, und
... den Koordinaten des Zentrums.
4.2.3 Beispiel:
Als Beispiel für die Realisierung in 3 Dimensionen soll hier der Mode mit l=3 und m=2 gezeigt werden. Dieses Beispiel entspricht dem Source-Code einer IDL-Routine. Die benötigte Dichtefunktion für die Mode ist folgendermaßen gegeben:
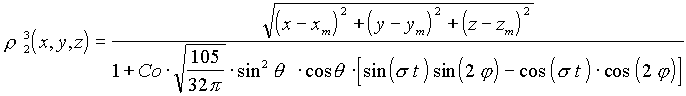
wobei die Polarkomponenten wie folgt umgerechnet werden können:
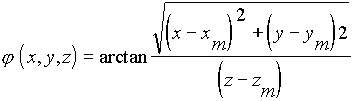
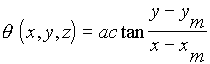
Um das Volumen für jeden Zeitpunkt zu berechnen haben wir 4 Schleifen: Die übergeordnete Zeitschleife und die 3 Unterschleifen über die Raumdimensionen x, y und z.
Um Rechenzeit zu sparen kann die Dichtefunktion in verschiedene Komponenten zerlegt werden. Zum einen in Komponenten die nur von der Zeit abhängen. Diese Terme brauchen nur für jeden Zeitpunkt berechnet werden und nicht für jeden Raumpunkt. Zum weiteren in Komponenten, die nur von der Zeit und den Raumdimensionen x und y abhängen. Diese Terme werden nur in der x und y Schleife berechnet. Und schlußendlich in jene Teile, in die sämtliche Parameter einfließen und immer neu berechnet werden müssen.
PRO l3m2
; Amplitudenfaktor, etwa 1000 mal höher als in der Realität
ko=1.0219855*0.6
; Variablen für das Volumen und Dichte für ISO-Oberfläche
Max=51.0 & Mitte=25.0 & Dichte=14.0
; Zeitschleife
FOR j=Anfangsbild,(Anfangsbild+Bilderanzahl-1) DO BEGIN
; Phase bestimmen
phase=(j+Anfangsphase*BilderJeZyklus) MOD BilderJeZyklus
; Terme bestimmen, die nur zeitabhängig sind
sigmat = - phase/BilderJeZyklus*2.0*pi & csst=COS(sigmat) & snst=SIN(sigmat)
; Schleife über die x-Achse
FOR x=0,(max-1) DO BEGIN
xmi=x-Mitte
; Schleife über die y-Achse
FOR y=0,(max-1) DO BEGIN
ymi=y-Mitte
phi=ATAN(ymi/xmi)
; Terme die nur von x und y abhängig sind
hilf1=(xmi)^2+(ymi)^2 & hilf2=SQRT(hilf1) & hilf3=COS(m*phi)
hilf4=SIN(m*phi) & hilf5=-csst*hilf3+snst*hilf4
FOR z=0,(max-1) DO BEGIN
zmi=z-Mitte
theta=ATAN(hilf2/zmi)
stern(x,y,z)=(SQRT(hilf1+(zmi)^2))/(1.0+ko*SIN(theta)^2.0*COS(theta)*hilf5)
ENDFOR
ENDFOR
ENDFOR
; ISO-Oberfläche berechnen
SHADE_VOLUME, stern,dichte,V,P
SCALE3,XRANGE=[0,max],YRANGE=[0,max],ZRANGE=[0,max]
; Raytracing und Ausgabe als 2d-Bild
bild=POLYSHADE(V,P,/T3D)
TV, bild
WRITE_Bmp,filename,bild,r,g,b
ENDFOR
END