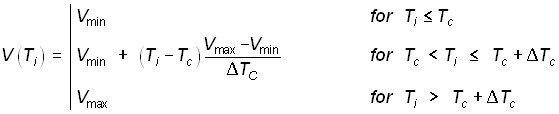 (2)
(2)Further information: Interessengemeinschaft
Geruch igG
published in:
Abstract
The diurnal and annual variation of distances for different odour thresholds is investigated by the dynamic Austrian odour dispersion model (AODM) consisting of an emissions module, a dispersion module, and a module to calculate instantaneous concentrations. Daily variations of the odour emission in parallel to the total heat release of the animals and the ventilation rate depending on the characteristics of the control unit of the ventilation system and the calculated indoor temperature are taken into account. The ambient half-hour odour concentrations calculated by a regulatory Gauss model are transformed to instantaneous values representative for the duration of a single breath by an attenuation function decreasing the peak-to-mean ratio with increasing wind speed, stability, and distance from the source.
Odour emission model
The emission model is based on a steady-state balance of the sensible heat fluxes to calculate the indoor temperature and the related volume flow of the ventilation system. The corresponding odour flow is assessed by a simple model of the odour release. The model has been described extensively in Schauberger et al. (1999a and 1999b), and therefore only its main features are reported here.
The air temperature inside a mechanically ventilated livestock building is calculated by using a balance equation of the sensible heat (Schauberger, 1988; CIGR 1984, Albright, 1990, ASHRAE, 1972; Sallvik and Pedersen, 1999). The indoor air temperature (equal to the temperature of the outlet air) and the volume flow are calculated as a function of the outdoor temperature.
The balance equation (Eqn 1) consists of three terms describing the sensible heat flux of the livestock building as
The ventilation systems in livestock buildings are mainly designed as temperature-controlled variable volume flow systems. The control unit uses the indoor air temperature as the control value. The supply voltage of the fans and therefore the resulting volume flow is the output of the control unit. Two parameters, the set point temperature TC and the proportional range DTC describe the course of the volume flow depending on the indoor air temperature Ti as a control value (eg Bruce, 1999). For an indoor air temperature less than the set point temperature, the minimum volume flow is supplied. In the proportional range above the set point temperature, the volume flow is increased until the maximum ventilation rate is reached. Above this range, the livestock building is supplied by the maximum ventilation flow. Equation (2) gives the volume flow V as a function of the indoor air temperature Ti.
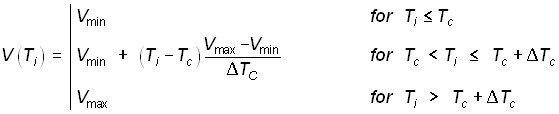 (2)
(2)| Parameter | |
| Mean total energy release of an animal QA (continuous fattening between 30 and 100 kg) |
|
| Minimum volume flow Vmin. Design value for the ventilation system taking into account the maximum accepted indoor CO2 concentration of 3000 ppm |
|
| Maximum volume flow Vmax. Design value for the ventilation system taking into account the maximum temperature difference between indoor and outdoor for summer (Ti=30°C) of 3 K |
|
| Area of the building (ceiling, walls, windows, doors) per animal |
|
| Thermal transmission coefficient U |
|
| Set point temperature of the control unit TC |
|
| Bandwidth of the control unit DTC |
|
The model calculations were done for a pig fattening unit of 1000 pigs with a forced ventilation. The livestock building is moderately isolated, described by the U value (Table 1). The assumed space per animal is 0.75 m² according to the welfare guide lines. The chosen system parameters for a livestock building with these specifications, typical for middle Europe, are summarised in Table 1.
The odour release from the livestock building originates from the animals, polluted surfaces and the feed. Outdoor odour sources such as slurry tanks or feed storage facilities are not taken into account. The emission of the livestock building at the outlet air is quantified by the odour flow E in OU/s and the specific odour flow e in OU/s LU related to the livestock (livestock unit (LU) equivalent to 500 kg live mass of the animals). The specific odour flow depends on the kind of animals and how they are kept. Available data are summarised by a literature review of Martinec et al. (1998). For the model calculation presented here, a mean specific odour flow em of 100 OU/s LU and a mean live mass of 60 kg per fattening pig (M = 0.12 LU) were used.
As odour production is a biochemical process, the temperature has an important influence. Most authors select the appropriate value for the outdoor air temperature To (Oldenburg, 1989; Kowalewsky, 1981). The linear regression of Oldenburg (1989) was adapted to assess the influence of the temperature T0 on odour flow Em by Eqn (3).
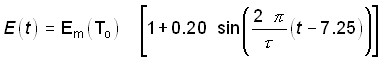 (4)
(4)The concentration of odoriphores can be handled like other volatile pollutants The dispersion of such substances can be described by well-known dispersion models, like a Gaussian one (e. g. Kolb, 1981; ÖNorm M 9440, 1992/96). Then the concentration at a receptor point is calculated as a mean value of the concentration of odoriphores for a defined period (e.g. half-hour, 3-hours mean value). The calculation of the odorant concentration itself is not meaningful if odour has to be evaluated. This is due to the fact that odour is not an attribute of an odoriphor, but a reaction of humans (Summer, 1970). To apply a dispersion model to odour emissions, the odour concentration and the volume flow of the outlet air have to be known. In many cases, these two parameters are assumed to be constant over time, although it is well known that the ventilation system of animal houses is designed to vary the air exchange in a range of 1:5 to 1:10 between the minimum and the maximum volume flow (Table 1, Vmin:Vmax=1:5). This time, appropriate variations of these parameters are taken into account (section 2.1).
The odour concentration of the centre line of the plume is calculated by the Austrian regulatory dispersion model (ÖNorm M 9440, 1992/96; Kolb, 1981) by making use of a statistics of stability classes representative for the Austrian flatlands north of the Alps. The model has been validated internationally with generally good results (e.g. Pechinger and Petz, 1995).
The regulatory model is a Gaussian plume model applied for single stack emissions and distances up to 15 km. Plume rise formulae used in the model are a combination of formulae suggested by Carson and Moses (1969) and Briggs (1975). The model uses a traditional discrete stability classification scheme with dispersion parameters developed by Reuter (1970).
The Austrian flatlands north of the Alps (200 to 400 m above sea level) are characterised by a moderate climate with both maritime and continental influences. The annual average temperature is 9 to 10°C. Precipitation occurs all the year round, culminating in summer storms, and yearly precipitation totals amount from 700 to 1000 mm from east to west. In general, there is a good ambient air movement, with mean wind speeds ranging from about 2 to 4 m/s. Except for north-south oriented valleys, main wind directions are west and east.
 a
a
 b
b
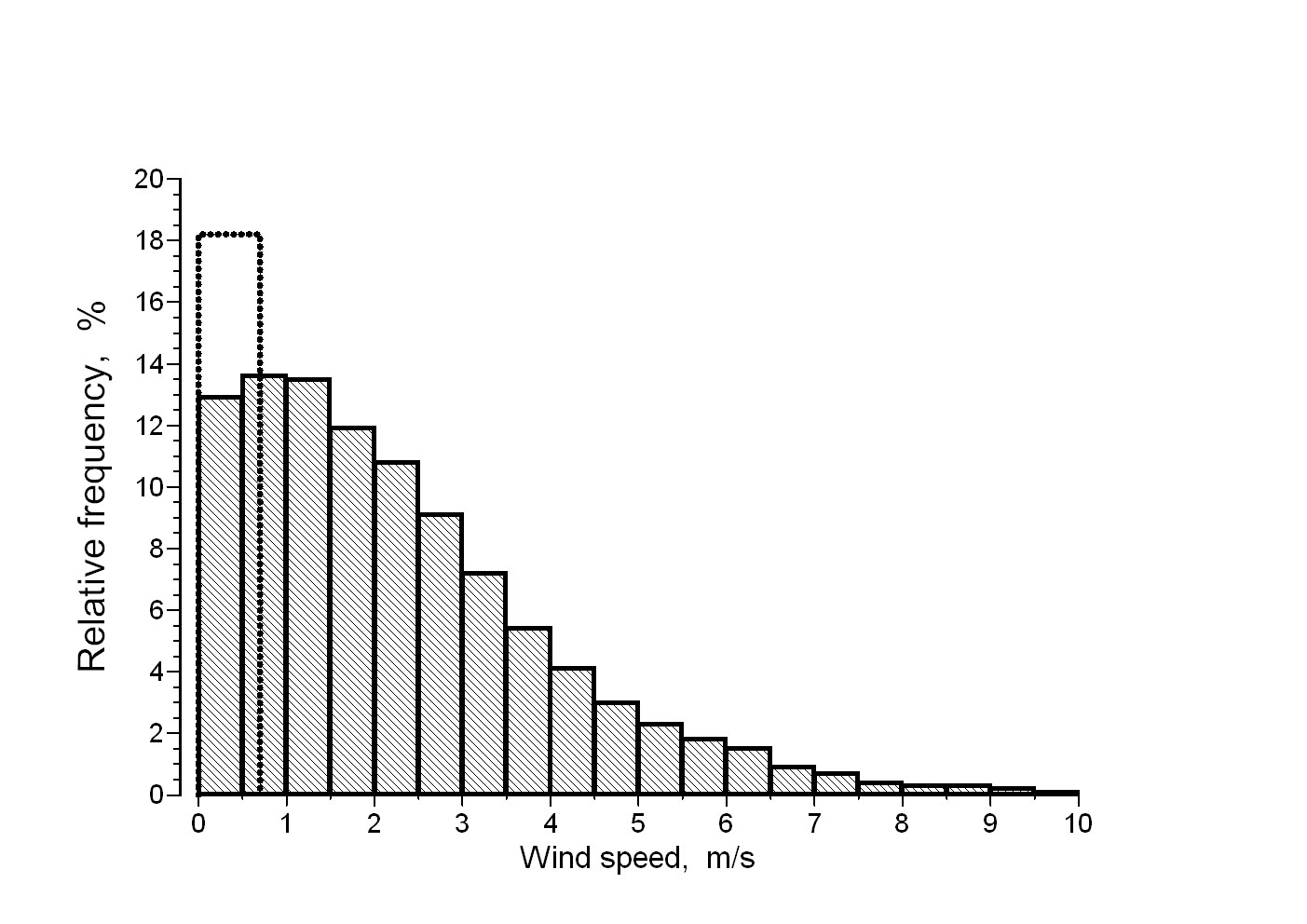
Fig. 1. Frequency distribution of (a)
the wind direction and (b) wind speed at Wels;
- - - - - -, Calm conditions according
to the Austrian regulatory dispersion model with wind speed less than 0.7
m/s (ÖNorm, 1992/1996).
Stability classes SC are determined
as a function of half-hourly mean wind speed and a combination of sun elevation
angle and cloud cover (Table 2). The cloud cover was monitored by the meteorological
station at the airport Linz-Hörsching, in a distance of about 13 km.
Within the Reuter scheme, classes 2 to 7 can occur in Austria. As seen from
Table 2, some combinations of stability class and wind speed are not possible
by definition (ÖNorm M 9440, 1992/1996). Stability class 4, representative
of cloudy and/or windy conditions including precipitation or fog, is by far
the most common dispersion category because it occurs day and night. Its
occurrence peaks at wind speeds of 2 and 3 m/s. Wind speeds larger than 6
m/s are almost entirely connected with class 4 (since a frequency of 1‰ is
equal to about 17 half hours in the two-year statistics, smaller occurrences
do not show up in Table 2). Stability classes SC=2 and SC=3, which by definition
occur only during daylight hours in a well-mixed boundary layer, class 3
allowing also for cases of high wind velocity and moderate cloud cover, peak
slightly below or around the average wind speed. They cover 26% of all cases.
Class 5 occurs with higher wind speeds during nights with low cloud cover,
a situation which is not observed frequently at Wels. Classes 6 and 7 are
relevant for clear nights, when a surface inversion, caused by radiative
cooling, traps pollutants near the ground. Such situations occur in 25% of
all cases.
|
|
|||||||
|
in m/s |
|
|
|
5 | 6 | 7 | |
|
|
|
|
|
41 | 71 | ||
|
|
|
|
|
35 | 59 | ||
|
|
|
|
|
30 | 22 | 7 | |
|
|
|
|
|
25 | 12 | ||
|
|
|
|
|
4 | |||
|
|
|
|
|||||
|
|
|
||||||
|
|
|
||||||
| Sum |
|
|
|
59 | 110 | 137 | |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The average occurrence of stability classes for each month is given in Table 3.
Table 3 shows a lot of seasonal variation of the occurrence of stability classes. Especially the probability for stability class 2 is about ten times higher during summer than during winter months. The effect of this variation on the distance, where sensation occurs, is discussed in section 3. The occurrence frequencies for stability classes 3 and 4 vary by a factor of 3, those for classes 5 to 7 by a factor of about 2.
Assessment of the expected maximum concentration in an interval of an breath
The regulatory model calculates half hour mean concentrations. The sensation of odour, however, depends on the momentary odour concentration and not on a mean value over a long time of integration. Smith (1973) gives the following relationship:
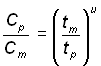 (6)
(6)These values are only valid close to the odour source. Due to turbulent mixing, the peak-to-mean ratio is reduced with increasing distance from the source. Mylne and Mason (1991) analysed the fluctuation of the plume concentration and developed the following relationship: The peak-to-mean ratio in equation (6) is modified by an exponential attenuation function of T/tL, where T=x/u is the time of travel with the distance x and the mean wind speed u, and tL is a measure of the Lagrangian time scale (Mylne, 1992):
 (7)
(7)The time scale tL is
taken to be equal to s/ewhere ![]() is the variance of the wind speed as the mean of the three wind components
u, v, and w, respectively, and eis the rate of dissipation
of turbulent energy using the following approximation:
is the variance of the wind speed as the mean of the three wind components
u, v, and w, respectively, and eis the rate of dissipation
of turbulent energy using the following approximation:
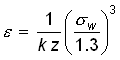 (8)
(8)|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The peak concentration Cp is calculated by the following equation:
 a
a
 b
b
 c
c
 d
d
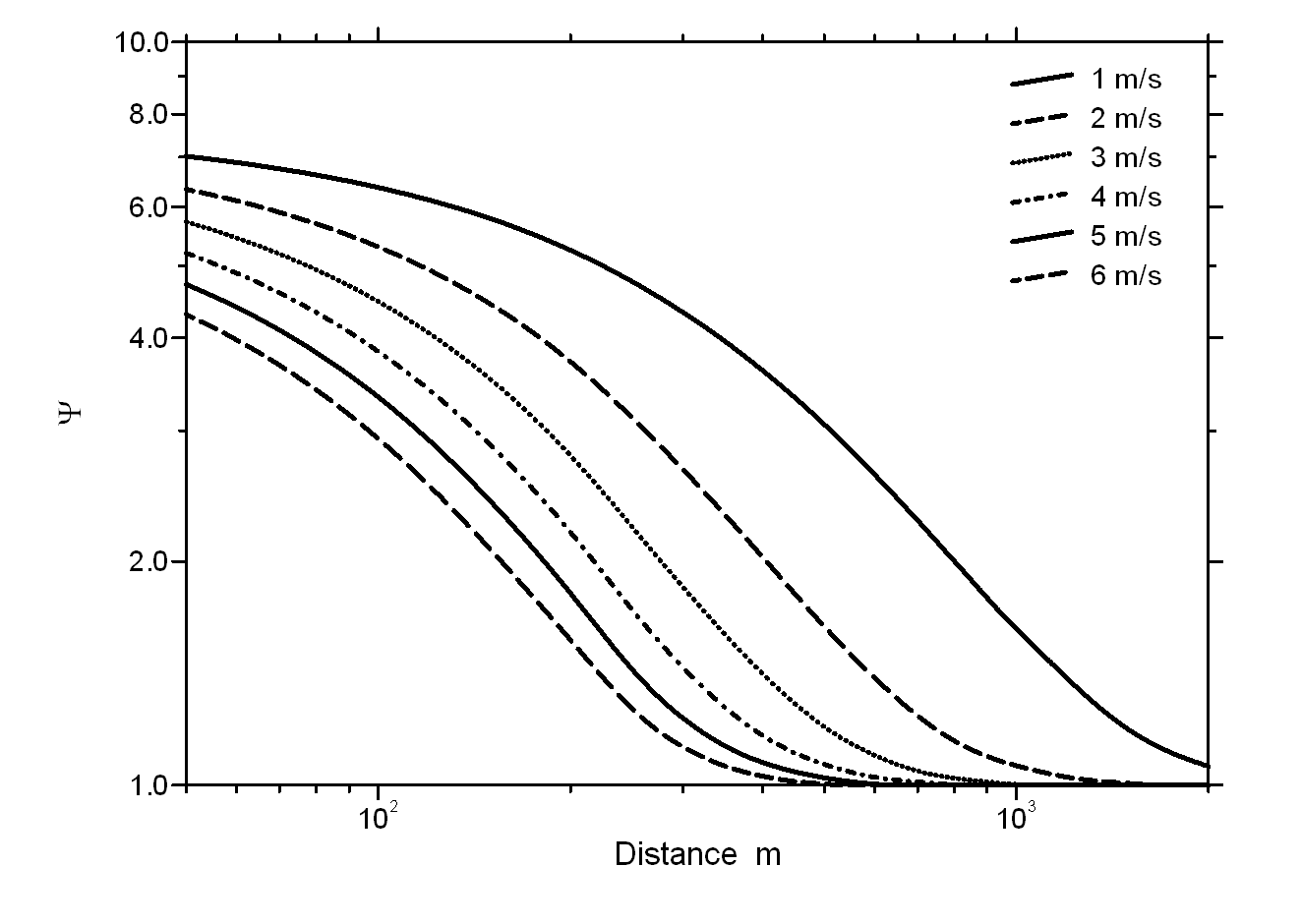
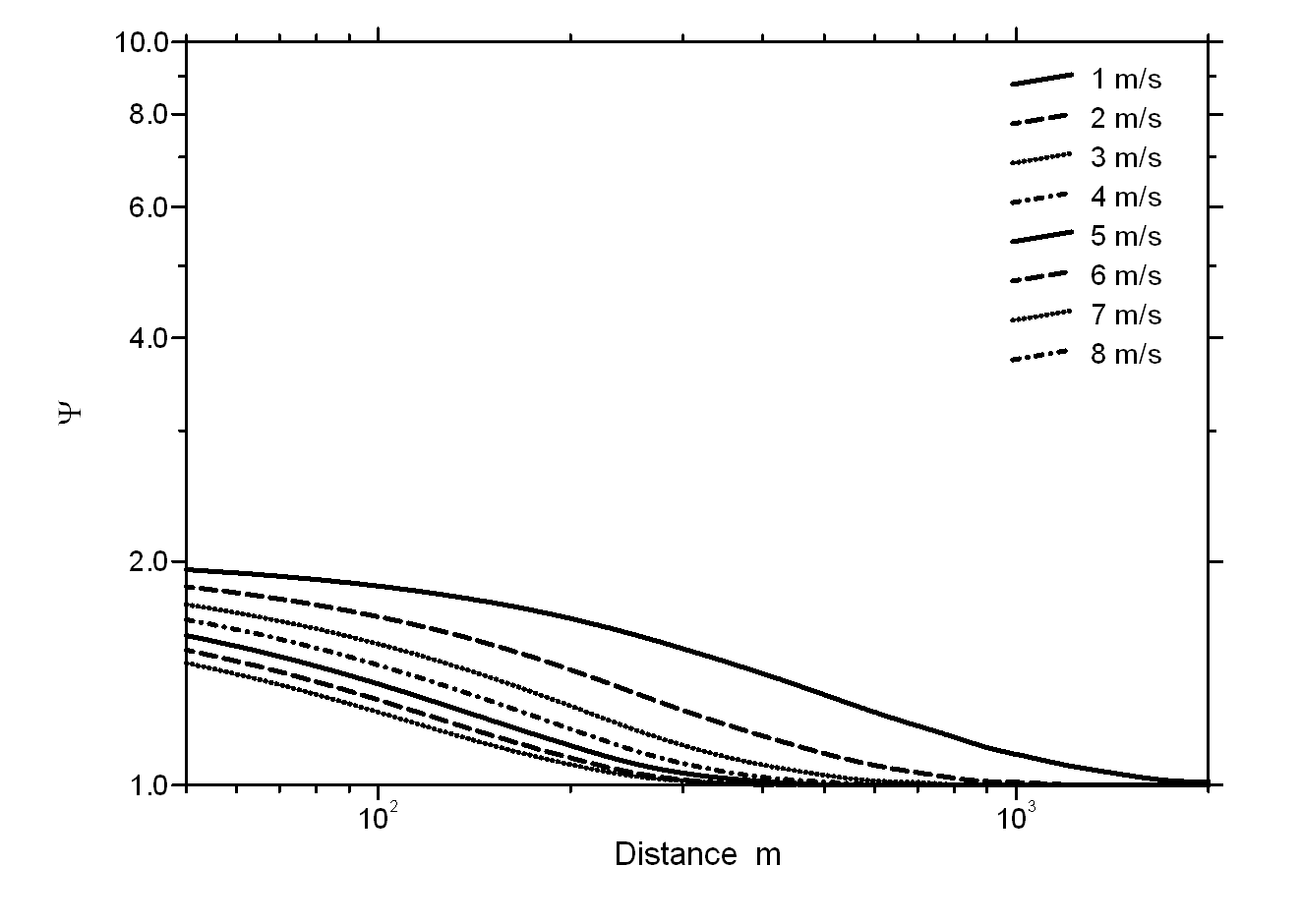
Fig. 2: Dependance of the attenuation
function Y of
the peak to mean ratio with distance for stability class 2 (a), 3 (b), 4
(c) and 5 (d) for all classes of wind velocity which occur at Wels (see also
Tab. 2 and 3)
Acknowledgement
This work was partly funded by the Austrian Federal Ministry for Environment, Youth and Family (GZ. 14 4444/10-I(4/29.
References
ASHRAE 1972. Handbook of Fundamentals. Environmental control for animals and plants – physiological considertaions. Am Soc of Heating Refrigerating and Air Conditioning Engineers. Cromwell, Conneticut. p 151-166.
Briggs, G. A. 1975. Plume rise predictions. Lectures on air pollution and environmental impact analysis, AMS, Boston, pp. 59 - 111.
Bruce, J.M. 1999. Environmental control of livestock housing. In: Houssine Bartali, E., Jongebreur, A., Moffitt, D. (eds): CIGR Handbook of Agricultural Engineering. Volume II: Animal Production & Aquacultural Engineering. ASAE, St. Joseph, Minnesota. p 54-87.
Carson, J., Moses, H. 1969. The validity of several plume rise formulas. J. Air Poll. Contr. Ass., 19, 862 - 866.
CIGR Commission International du Genié Rural 1984. Climatization of animal houses. Scottish Farm Buildings Investigation Unit, Aberdeen, Scottland
CIGR Commission International du Génie Rural 1994. Aerial environment in animal housing - concencentration in and emission from farm buildings. CEMAGREF, Rennes
Hoff, S. J., Bundy, D S., Li X W 1997. Dust effects on odor and odor compounds. In: Ammonia and Odour Emission from Animal Production Facilities (Voermans, J., A., M., Monteny, G., J., eds), p677-684, Rosmalen, The Netherlands
Kolb, H. 1981. Ein normatives Modell zur Simulierung der Ausbreitung von Schadstoffen in der Atmosphäre unter besonderer Berücksichtigung der Verhältnisse in Österreich. [A regulative model to simulate the dispersion of pollutants in the atmosphere for the situation in Austria]. Publ. 29. Abteilung für Theoretische Meteorologie, University Vienna, Vienna
Kowalewsky, H. H. 1981. Messen und Bewerten von Geruchsimmissionen. Chemische und sensorische Bestimmung des Geruchs in der Umgebung von Ställen, offenen Füllbehältern und begüllten Feldern [Measuremenrt and evaluation of odour concentration. Chemical and sensorial evaluation of odour in the vicinity of livestock housings, open slurry tanks and fields dunged with slurry]. KTBL-Schrift 260, Kuratorium für Technik und Bauwesen in der Landwirtschaft e.V. KTBL,. Darmstadt
Martinec, M., Hartung, E., Jungbluth, Th. 1998. Geruchsemissionen aus der Tierhaltung (Literaturstudie. [Odour emission of livestock husbandry (a literature survay)]. pp68, Ministerium für Umweld und Verkehr, Baden-Würthenberg, Germany
Misselbrook, T.H., Clarkson, C.R., Pain, B.F. 1993. Relationship between concentration and intensity of odour for pig slurry and broiler houses. J of Agricultural Engineering Research 55: 163-169
Mylne, K.R. 1988. Concentration fluctuation measurements of a tracer plume at up to 1 km range in the atmosphere. 9th Symp. on Turbulence and Diffusion, Roskilde, p168-171.
Mylne, K.R. 1992. Concentration fluctuation measurements in a plume dispersing in a stable surface layer. Boundary-Layer Meteorology60, 15-48.
Mylne, K.R., Mason P.J. 1991. Concentration fluctuation measurements in a dispersing plume at a range of up to 1000m. Quart. J Royal Meteorol Soc. 117, 177-206.
Nicell, J. A. 1994. Development of the odour impact model as a regulatory strategy. Int. J. Environment and Pollution 4, 124-138.
Oldenburg, J. 1989. Geruchs- und Ammoniak-Emissionen aus der Tierhaltung [Odour and ammonia emission of livestock husbandry]. KTBL-Schrift 333, Kuratorium für Technik und Bauwesen in der Landwirtschaft e.V. KTBL, Darmstadt
ÖNorm M 9440 1992/1996. Ausbreitung von luftverunreinigenden Stoffen in der Atmosphäre; Berechnung von Immissionskonzentrationen und Ermittlung von Schornsteinhöhen [Dispersion of pollutants in the atmosphere – calculation of the ambient air concentrations and determination of stack heights]. Österreichisches Normungsinstitut, Vienna
Pechinger, U., Petz, E. 1995. Model evaluation of the Austrian Gaussian plume model ON M 9440: comparison with the Kincaid dataset. Int. J. Environment and Pollution 5, 338 - 349.
Pedersen, S. 1993. Time based variation in airborne dust in respect to animal activity. In: 4th International Livestock Environmental Symposium (Collins E., Boon C eds), Coventry, England
Pedersen, S. 1996. Døgnvariationer i dyrenes aktivitet i kvæg-, svine- og fjerkræstalde [Diurnal variation of the animal activity of calve, pig and poultry]. Internal report 66. Danish Institute of Animal Science. Horsens, Denmark
Pedersen, S., Pedersen, C., B. 1995. Animal activity measured by infrared detectors. Journal of Agricultural Engineering Research, 61, 239-246
Pedersen, S., Rom, H., B. 1998. Diurnal variation in heat production from pigs in relation to animal activity. International Conference on Agricultural Engineering AgEng 98, Oslo, Norway
Pedersen, S., Takai, H. 1997. Diurnal Variaton in animal heat production in relation to animal activity. In: 5th International Livestock Environmental Symposium (Bottcher R W., Hoff St J eds) Bloomington, Minnesota
Phillips, V. R., Holden, M. R., Sneath, R. W., Short, J. L., White, R. P., Hartung, J., Seedorf, J., Schröder, M., Linkert, K. H., Pedersen, S., Takai, H., Johnsen, J. O. P., Groot Koerkamp, W. G., Uenk, G. H., Scholtens, R., Metz, J. H. M., Wathes, C. M. 1998. The development of robust methods for measuring concentrations and emission rates of gaseous and particulate air pollutants in livestock buildings. Journal of Agricultural Engineering Research, 70,11-24
Piringer, M., Schauberger, G 1999. Comparison of a Gaussian Diffusion Model with Guidelines for Calculating the Separation Distance between Livestock Farming and Residential Areas to Avoid Odour Annoyance. Atmospheric Environment, 33 2219–2228
Piringer, M., Schauberger, G. 1999. Comparison of a Gaussian diffusion model with guidelines for calculating the separation distance between livestock farming and residential areas to avoid odour annoyance. Atmospheric Environment, 33, 2219–2228.
Reuter, H. 1970. Die Ausbreitungsbedingungen von Luftverunreinigungen in Abhängigkeit von meteorologischen Parametern [Dispersion conditions of airborne pollutants in dependence on meteorological parameters]. Archiv für Meteorologie und Geophysik, Bioklimatologie A 19, 173-186
Rieß, G., Maier, B., Neser, St., Zeisig, H.-D., Gronauer, A., Schön, H. 1999. Bewertung von Geruchsemissionen verschiedener Tierhaltungssysteme mittels Multisensorarray am Beispiel von Mastschweinehaltungen mit Ober- und Unterflurabsaugung. In: Bau, Technik und Umwelt 1999, München-Weihenstephan, Germany.
Robins, A. G. 1979. Development and structure simulated neutrally simmulated boudary layers. J. Ind. Aerodyn. 4, 71-100.
Sallvik, K. 1999. Animal Environment Requirements. In: Houssine Bartali, E., Jongebreur, A, Moffitt, D (Eds): CIGR Handbook of Agricultural Engineering. Volume II: Animal Production & Aquacultural Engineering. ASAE, St. Joseph, Minnesota. p 31-41.
Sallvik, K., Pedersen, S. 1999. Animal heat and moister production In: Houssine Bartali, E., Jongebreur, A., Moffitt, D. (eds): CIGR Handbook of Agricultural Engineering. Volume II: Animal Production & Aquacultural Engineering. ASAE, St. Joseph, Minnesota. p 41-54.
Schauberger, G. 1988. Ein quasi-stationäres Bilanzmodell zur Stallklima-Simulation [A steady-state balance model to simulate the indoor climate in livestock buildings]. Deutsche Tierärztliche Wochenschrift, 95, 200 - 205
Schauberger, G. 1989. Computersimulation des Stallklimas am PC in der tierärztlichen Praxis [Computer simulation of the indoor climate in livestock buildings on the PC]. Berliner und Münchner Tierärztliche Wochenschrift, 102, 58 - 63
Schauberger, G., Pilati, P. 1998a. Evaluation of a steady-state balance model to simulate the indoor climate inside livestock buildings: a comparison with measurements of a cattle house. International Conference on Agricultural Engineering AgEng 98, Oslo, Norway
Schauberger, G., Pilati, P. 1998b. Evaluierung eines quasi-stationären Bilanzmodells zur Stallklimasimulation: Vergleich mit Messungen eines Rindermaststalles [Evaluation of a steady-state balance model to simulate the indoor climate in livestock buildings: a comparison with measurements of a cattle house]. Wiener Tierärztliche Monatsschrift, 85, 49-55
Schauberger, G., Piringer, M., Petz, E. 1999a. Diurnal and annual variation of odour emission of animal houses: a model calculation for fattening pigs. Journal of Agricultural Engineering Research in print
Schauberger, G., Piringer, M., Petz, E. 1999b. Steady-state balance model to calculate the indoor climate of livestock buildings demonstrated for fattening pigs. International Journal of Biometeorology, submitted
Schiffman, S. S. 1998. Livestock Odors: implications for human health and well-being. Journal of Animal Science 76, 1343 - 1355
Smith, M.E. 1973. Recommended Guide for the Prediction of the Dispersion of Airborne Effluents. ASME, N.Y.
Summer, W. (1970): Geruchlosmachung von Luft und Abwassser. Oldenburg München